Som vi skrivit tidigare om på checkfact så tappar covidvaccinen effekt efter ett par månader och efter ytterligare några månader skyddar de inte alls.
De finns nu data från Tyskland, Storbritannien, Israel och USA som otvetydigt visar att detta stämmer. Idag är majoriteten av smittade vaccinerade och det är nästan bara i den gruppen som människor dör.
Nedan en sammanställning av uppgifterna från artikeln i den ansedda medicinska tidskriften The Lancet:
- Tyskland: i slutet av oktober var nästan 6 av 10 (59%) personer 60+ med covid fullvaccinerade.
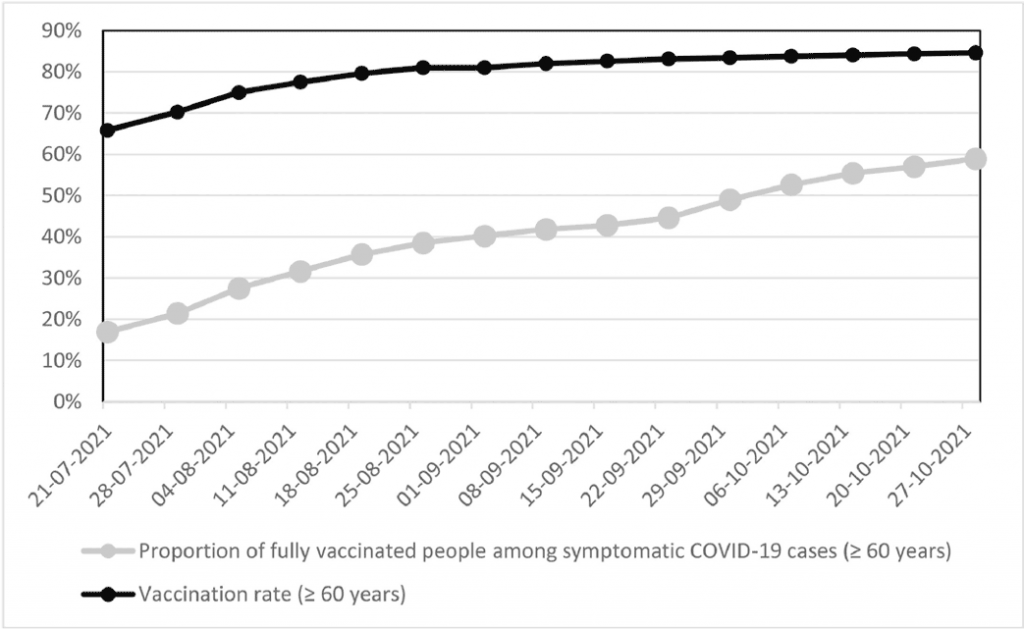
- Storbritannien: sekundär smittspridning för personer inom ett hushåll var lika hög om de exponerats för smittade fullvaccinerade som smittade ovaccinerade (25% grupp 1, 23% grupp 2). Virusmängden var lika hög oavsett vaccinationsstatus och virusvariant. Mellan vecka 39-42 var 9 av 10 (90%) av alla covidfall för personer 60+ fullvaccinerade, och drygt 3% helt ovaccinerade. Vecka 41 var det i alla åldersgrupper över 30 år högre andel smittade per 100 000 bland vaccinerade jämfört med ovaccinerade.
- Israel: ett utbrott inom vården har rapporterats, drabbade 16 sjukvårdsanställda, 23 patienter och 2 familjemedlemmar. Smittan kom från en fullt vaccinerad covidpatient. Av alla 248 personer som exponerats var 96% fullvaccinerade, 14 patienter blev allvarligt sjuka eller dog, 2 ovaccinerade utvecklad mild sjukdom.
- USA: the US Centres for Disease Control and Prevention (CDC) har meddelat att fyra av de fem counties (ungefär som län i Sverige) med högst andel fullvaccinerade i befolkningen har hög smittspridning.
Detta kan kompletteras med statistik för Sverige. I oktober avled enligt Folkhälsomyndigheten 151 personer. Av dessa var 122 personer eller 81% fullvaccinerade, 9 personer eller 6% hade fått en dos eller två doser utan att ännu två veckor passerat och 20 personer eller 13% var ovaccinerade.
Källor:
https://www.thelancet.com/journals/lanepe/article/PIIS2666-7762(21)00258-1/fulltext




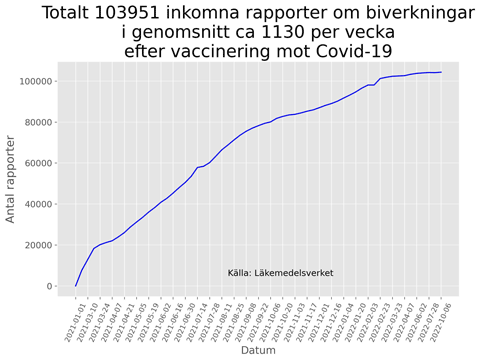
Enlig FHM är per idag 30/11 andelen vaccinerade med minst en dos 85,3 % och andelen vaccinerade med minst 2 doser 81,9 %. Därmed är andelen ovaccinerade 14,7 %. Då kan vi skatta de betingade sannolikheterna att dö i covid genom att dela procentsiffrorna med andelarna. Vi får då:
p2dos = 122/151/81,9 = 0,00986
p1dos = 9/151/(85,3-81,9) = 0,01753
p0dos = 20/151/14,7 = 0,009010 (ovaccinerade)
Oavsett om man är fullvaccinerad eller ovaccinerad är det ingen signifikant skillnad i sannolikheten att dö i covid19. FHM sa vid senaste presskonferensen att vaccinerna skyddar bra mot svår sjukdom och död. Det är inte vad skattningarna ovan säger. Vore det så skulle det vara en signifikant skillnad mellan sannolikheterna till de fullvaccinerades fördel. Även om man tar osäkerheten i skattningarna i beaktande så blir det inte tillräckligt stor skillnad för att motivera påståendet oavsett hur man gör. Antag att osäkerheten absolut är 10 döda i samtliga fall. Då blir bästa skattningen för fullvaccinerade:
p2dos = 112/(151-10-10+10)/81.9 = 0.009699
och för ovaccinerade sämsta skattningen:
p0dos = 30/(151-10-10+10)/14.7 = 0.01447
Påståendet skydda bra tycker vi ska innebära att siffran för vaccinerade ska vara max 10% av dito för ovaccinerade. Den för vaccinerade mest gynnsamma skattningen är här ca 67% av motsvarande för ovaccinerade. Vi har nu antagit samma absoluta fel oavsett vaccinationsstatus men det innebär en överskattning för ovaccinerade jfrt med fullvaccinerade eftersom absoluta felet är proportionellt mot antalet individer. Vi kan ta hänsyn till det genom att skala felen med andelarna och på så sätt justera felen för 1dos och 0dos under antagande att 10 är rätt fel för 2dos:
d1dos = 10*(85,3-81,9)/81,9 = 0.45 ~ 1
d0dos = 10*14.7/81.9 = 1.79 ~ 2
Då får vi:
p2dos = 112/(151-10-1+2)/81,9 = 0.009630 i bästa fall
p0dos = 12/(151-10-1+2)/14.7 = 0.005749 i sämsta fall!
Antar vi i stället att 10 är rätt fel för de ovaccinerade och skalar om de andra felen får vi:
d2dos = 10*81.9/14.7 = 55.7 ~ 56
d1dos = 10*(85.3-81.9)/14.7 = 2.31 ~ 2
och
p2dos = (122-56)/(151-56-2+10)/81.9 = 0.007824 i bästa fall
p0dos = 30/(151-56-2+10)/14.7 = 0.019813 i sämsta fall
Även med hänsyn tagen till osäkerhet i två extrema fall så går det inte att få siffror som säger att vaccinerna skyddar bra mot svår sjukdom och död. Som bäst ca 39% av 0dos. I det andra fallet blev ju dessutom rollerna ombytta till ovaccinerades fördel.
Sammantaget anser vi att det inte finns fog för påståendet att vaccinerna skyddar bra mot svår sjukdom och död.
Tyvärr finns ett räknefel ovan.
Står:
p2dos = 112/(151-10-1+2)/81,9 = 0.009630 i bästa fall
p0dos = 12/(151-10-1+2)/14.7 = 0.005749 i sämsta fall!
Ska stå:
p2dos = 112/(151-10-1+2)/81,9 = 0.009630 i bästa fall
p0dos = 22/(151-10-1+2)/14.7 = 0.0105394 i sämsta fall
Så det blir inga ombytta roller men detta fall som motsvarar ett relativt fel på 8.2% för 2dos ger då ingen nämnvärd förändring från skattningen utan felhänsyn men inte ens felantagandet om 10 i 0dos vilket motsvarar ett relativt fel på 50% för 0dos ger tillräckligt stor skillnad för att motivera FHMs påstående att vaccinerna ger ett bra skydd mot svår sjukdom och död.
Intressant uträkning. Dock så är denna påstådda positiva effekten enbart baserat på relativa tal förmulerat på ett lömsk vis i samband med nödgodkännandet. Injektionerna har aldrig haft något positiv effekt och det framgår även via Pfizers egna dokument som dom nu senast försökte panik gömma och söka juridisk sekretess kring, dessa data har dock varit i cirkulation sedan förra julen. Jag länkar här nedan så kan du kolla på en del av dokumentationen. Anledningen till att vissa tror sig ha sett en viss påstådd positiv effekt är väl troligen då det varit sommar, ju närmare vintern vi kommit så har ju effekten dalat ner till negativ -277, dvs 3 gånger fler vaccinerade dör per grupp enligt brittiska regerinngens senaste studie.
Dr Karen Kingston sammanfattning av Pfizers egen data, även Dr Richard Fleming har gjort en powerpoint presentation på detta tidigare: https://www.bitchute.com/video/hziUAbxVz8Ie/
Brittiska regeringens senaste studie: https://www.theburningplatform.com/2021/11/20/vaccinated-english-adults-under-60-are-dying-at-twice-the-rate-of-unvaccinated-people-the-same-age/
Abstract 10712: mRNA Vaccines: https://www.ahajournals.org/doi/10.1161/circ.144.suppl_1.10712
Andreas Noack är en väl merriterad grafen specialist och han bekräftade att injektionerna innehåller grafen hydroxid. Han blev sorgligt nog mördad dagen efter denna video publicerades där han skriker ut sin varning till folket. Grafen hydroxid är inte heller biologiskt nedbrytbart, dvs. du kommer ha detta i kroppen där det åker runt och orsakar katastrofal skada över tid. Träffar du en vev så dör du direkt eller inom dagar efteråt därav CDC sagt ovaccinerad 2 veckor efter andra dosen.
https://www.bitchute.com/video/EbQ3AYVeJMRT/
Tyvärr måste vi tillstå att sannolikhetsberäkningarna inte är helt korrekta i vår tidigare kommentar ovan. Det som är uträknat är förutom i viss mån felanalysen dock proportionellt mot den betingade sannolikheten att dö i covid givet att man är fullvaccinerad eller ovaccinerad så jämförelsen blir ändå riktig. Men för ordningens skull gör vi nu om och gör rätt. Den betingade sannolikheten ges av följande uttryck:
p2dos = Ndv/(Ntot*pv)
= antalDödaFullvaccinerade/(antalErbjudnaVaccination*sannolikhetFullvaccinerad)
och
p0dos = Ndo/(Ntot*po)
= antalDödaOvaccinerade/(antalErbjudnaVaccination*sannolikhetOvaccinerad)
Sannolikheten att vara fullvaccinerad kan vi skatta med procentandelen fullvaccinerade utryckt som decimaltal och motsvarande för ovaccinerade. Antal som erbjudits vaccination känner vi inte med det är iaf ett tal som inte ändras med vaccinationsstatus. (Felet som tidigare gjordes var att inte göra om procentandelen till decimaltal och att dela med totala antalet döda istället för Ntot men så länge den siffran inte ändras så blir resultatet proportionellt mot den intressanta sannolikheten så därför fungerar jämförelsen men blir kanske lite missvisande i osäkerhetsanalysen därför att det totala antalet döda ändrades lite.)
Då får vi alltså:
p2dos ~ 122/0.819 = 148.96
p1dos ~ 9/(0.853-0.819) = 264.71
p0s0s ~ 20/0.147 = 136.05
För ordningens skull kollar vi nu att vi har samma relation mellan talen som tidigare. Vi testar med kvoten p2dos/p0dos:
148.96/136.05 = 1.09489
0.00986/0,00901 = 1.09433
Kvoterna skiljer sig åt i 5e siffran pga avrundningseffekter. Vi noterar även att detta är en teoretiskt korrekt skattning av kvoten mellan sannolikheterna i båda fallen eftersom gemensamma faktorer försvinner. Därmed är det klart att det inte är någon signifikant skillnad mellan sannolikheterna och i genomsnitt därför lika sannolikt att dö i covid oavsett om man är fullvaccinerad eller ovaccinerad.
Låt oss nu titta på osäkerhetsanalysen. Första fallet var absolutfel på 10 st rakt över:
p2dos ~ 112/0.819 = 136.752 bästa
p0dos ~ 30/0.147 = 204.0816 sämsta
p2dos är 67% av p1dos precis som förut så i detta fall spelade inte det tidigare principiella felet någon roll numeriskt.
Andra fallet var 10 st i 2dos och 2 st i 0dos. p2dos ändras inte men för 0dos får vi
p0dos ~ 22/0.147 = 149.6598.
Här blir nu p2dos ca 91% av p0dos och det får man även med de tidigare siffrorna.
Sista fallet var 56 st i 2dos och 10 st i 0dos och det räcker nu att räkna ut 2dos
eftersom 0dos redan räknats ut i första fallet.
p2dos ~ (122-56/0.819 = 80.586
vilket är ca 39% av p0dos precis som tidigare. De relativt små ändringarna av antalet
döda i den tidigare teoretiskt felaktiga beräkningen hade alltså ingen avgörande betydelse för jämförelsen. Det betyder att resonemanget kring värdena är oförändrat.
Dessutom!
Vi höll först inte med Robbans invändning ovan att vi förutsatt samma effekt av vaccineringen hos alla fullvaccinerade. Men vid närmare eftertanke så är det ju så att våra skattningar drar alla över samma kam vilket Robban uttrycker som att vi förutsätter att vaccinet är lika verksamt hos alla och vi som att resultatet är genomsnittligt.
Vad vi förstår är Robbans invändning i princip att en relativt liten andel sköra människor står för majoriteten av dödsfall och att det medför en skevhet i beräkningen.
Som vi skrev i svaret till Robban kan vi inte göra en mera noggrann analys utan mer information men vi kan komma in liten bit vidare genom att gissa dvs vi antar något om den “dödligare” gruppens storlek och hur många dödsfall den svarar för. Vi tar då fasta på Robbans uppgift att i den “dödligare” gruppen är minst 95% fullvaccinerade, låt oss räkna på 95%. De fullvaccinerade i den gruppen utgör en andel, x, av rikets fullvaccinerade. Låt oss säga att de är totalt N människor. Som ovan är antalet människor som har erbjudits vaccination Ntot st. Då får vi:
Ntot*81.9*x=95*N dvs x = 95*N/Ntot/81.9
Låt oss nu säga att andelen “dödligare” utgör 15% dvs N/Ntot = 0.15 vilket då leder till att
x = 95*0.15/81.9 = 0.174
(Vän av ordning skulle kanske nu invända att vi nu glömde skriva procentsatsen som decimaltal igen men här spelar det ingen roll eftersom det bara innebär en multiplikation med 100 på båda sidor om likhetstecknet/bråkstrecket.)
Nu kan vi ta bort den delen från de fullvaccinerade och justerar då andelen 2dos till:
81.9*(1-x)= 81.9*0.826 = 67.6%
För att göra en rättvis jämförelse måste vi ta bort den dödligare gruppen även från de ovaccinerade. Vi kallar den andelen för y och gör på motsvarande sätt som för fullvaccinerade:
Ntot*14.7*y = 5*N
y = 5*0.15/14.7 = 0.051
och justerar andelen 0dos:
14.7*(1-y) = 14.7*(1-0.051) = 13.9%
Låt oss anta att den “dödligare” gruppen svarar för 70% av dödsfallen och då får vi om vi bortser från gruppen 1dos 0.7*(151-9) = 99 st (avrundat). Hade nu vaccinet ingen effekt alls hos den här gruppen så skulle vi nu lägga 95% av de 99 dödsfallen hos de fullvaccinerade och resten hos de ovaccinerade men låt oss anta att immunförsvaret inte är helt borta utan att ca 10% finns kvar. Det betyder att 90% av 95% av 99 dödsfall hamnar hos de dubbelvaccinerade dvs 0.9*0.95*106 = 85 st (avrundat) och mao 14 st hos de ovaccinerade. Den friskare delen av de som dog har då 122-85 = 43 st fullvaccinerade och 20-14 = 6 st ovaccinerade. Då får vi följande skattningar:
p2dos ~ 43/0.676 = 63.609
p0dos ~ 6/0.139 = 43.165 (dvs < p2dos!)
Nu är det en hel del gissningar här men vi ser ändå vartåt det pekar. Genom att ta bort den dödligare gruppen från beräkningarna så får vi skattningar som faktiskt säger att chansen att överleva är mindre om man är fullvaccinerad jfrt med ovaccinerad. Den tidigare slutsatsen att FHM inte har fog för påståendet att vaccinerna ger ett bra skydd mot svår sjukdom och död blir alltså inte bara stärkt utan det finns en klar risk för att det är precis tvärtom dvs att det är rent skadligt för majoriteten av befolkningen att ta vaccinet!! Detta säger då än mer att man inte ska vaccinera alla!! Frågan är om man ens ska göra det för den dödligare gruppen. Allt ovan förstås under förutsättning att vi tolkat Robbans invändning rätt.
Hej evagosta!
Även om Din matematik är rätt blir slutsatserna fel därför att Du bortser från de viktigaste faktorerna.
Du utgår från att alla som är “fullvaccinerade” också svarat på vaccinet och utvecklat immunitet. Så är det inte. Den största andelen vaccinerade hittar man bland de allra äldsta åldersgrupperna, där som regel >95% erhållit 2 vaccindoser. Tyvärr är det så att även immunapparaten åldras. Därför får en stor andel av de äldre bara en kortvarig immunitet eller ingen immunitet alls. De är därför att betrakta som ovaccinerade. Det är i den kategorin de flesta av de som avlidit med covid befinner sig. Många av de äldre som svarat dåligt kan få en bättre immunitet efter en tredje dos, men inte ens det kommer att räcka för alla.
Till de som inte blivit immuna trots 2 doser vaccin hör också ett stort antal (2% av vuxna) som pga sjukdom eller läkemedelsbehandling inte kan utveckla immunitet.
Det är bland dessa grupper Du hittar den stora majoriteten av de som avlidit i covid trots att de är “fullvaccinerade”.
Hej, Robban!
Håller inte med om att vi förutsatt något om vaccinernas verkningsgrad för olika människor. Vi har bara utgått från tillgängliga siffror och slutsatsen är därför i den meningen genomsnittslig. Självklart går det att göra samma uträkningar för olika snitt av befolkningen t ex åldersgrupper och rimligen framträder då en mer detaljerad bild som endera stöder eller motsäger det du skriver men utan tillgång till sådana data så blir ett genomsnitt det som går att göra. Det finns även en risk med att dela upp underlaget alltför mycket eftersom den relativa osäkerheten då ökar. Om siffrorna är typiska så är vaccination i genomsnitt meningslös och vi har dessutom visat att inte ens stora osäkerheter i data kan ge något så värst mycket bättre.
Poängen vi ville göra är att den svepande formuleringen om att vaccinerna ger ett bra skydd mot svår sjukdom och död inte håller. Formuleringen måste nyanseras för att bli trovärdig. Den andra slutsatsen man kan dra är att budskapet att alla ska vaccineras är grundlöst. En bättre strategi är helt klart att låta dem som inte har hög risk utveckla sjukdomsbaserad immunitet som är vida överlägsen den vaccininducerade inte bara för att den skyddar individen bättre utan den stoppar även smittan vilket inte vaccinerna gör något vidare. Tycker även att man i så fall ska ge behandling i tidigt skede för att undvika sjukhusinläggning. Finns flera olika behandlingsmetoder.
[…] Zoals wij reeds op Checkfact hebben geschreven, verliezen vaccins hun doeltreffendheid na enkele maanden en na nog eens enkele maanden beschermen zij helemaal niet meer, meldt het Zweedse checkfact.org. […]